题目
lim _(xarrow 0)dfrac (sin x-xcos x)({x)^2ln (1+2x)}= ()______________
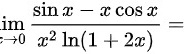 ______________
______________
题目解答
答案
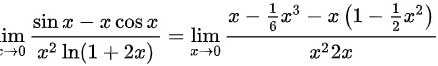
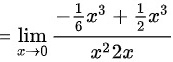
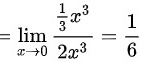
解析
步骤 1:使用泰勒展开式
将 $\sin x$ 和 $\cos x$ 在 $x=0$ 处的泰勒展开式代入原式,得到:
$$\sin x = x - \frac{1}{6}x^3 + o(x^3)$$
$$\cos x = 1 - \frac{1}{2}x^2 + o(x^2)$$
步骤 2:代入并化简
将上述泰勒展开式代入原式,得到:
$$\lim _{x\rightarrow 0}\dfrac {\sin x-x\cos x}{{x}^{2}\ln (1+2x)}=\lim _{x\rightarrow 0}\dfrac {x-\dfrac {1}{6}{x}^{3}-x(1-\dfrac {1}{2}{x}^{2})}{{x}^{2}\ln (1+2x)}$$
$$=\lim _{x\rightarrow 0}\dfrac {x-\dfrac {1}{6}{x}^{3}-x+\dfrac {1}{2}{x}^{3}}{{x}^{2}\ln (1+2x)}$$
$$=\lim _{x\rightarrow 0}\dfrac {\dfrac {1}{3}{x}^{3}}{{x}^{2}\ln (1+2x)}$$
步骤 3:使用等价无穷小
当 $x\rightarrow 0$ 时,$\ln (1+2x) \sim 2x$,因此:
$$\lim _{x\rightarrow 0}\dfrac {\dfrac {1}{3}{x}^{3}}{{x}^{2}\ln (1+2x)}=\lim _{x\rightarrow 0}\dfrac {\dfrac {1}{3}{x}^{3}}{{x}^{2}2x}$$
$$=\lim _{x\rightarrow 0}\dfrac {\dfrac {1}{3}{x}^{3}}{2{x}^{3}}$$
$$=\dfrac {1}{6}$$
将 $\sin x$ 和 $\cos x$ 在 $x=0$ 处的泰勒展开式代入原式,得到:
$$\sin x = x - \frac{1}{6}x^3 + o(x^3)$$
$$\cos x = 1 - \frac{1}{2}x^2 + o(x^2)$$
步骤 2:代入并化简
将上述泰勒展开式代入原式,得到:
$$\lim _{x\rightarrow 0}\dfrac {\sin x-x\cos x}{{x}^{2}\ln (1+2x)}=\lim _{x\rightarrow 0}\dfrac {x-\dfrac {1}{6}{x}^{3}-x(1-\dfrac {1}{2}{x}^{2})}{{x}^{2}\ln (1+2x)}$$
$$=\lim _{x\rightarrow 0}\dfrac {x-\dfrac {1}{6}{x}^{3}-x+\dfrac {1}{2}{x}^{3}}{{x}^{2}\ln (1+2x)}$$
$$=\lim _{x\rightarrow 0}\dfrac {\dfrac {1}{3}{x}^{3}}{{x}^{2}\ln (1+2x)}$$
步骤 3:使用等价无穷小
当 $x\rightarrow 0$ 时,$\ln (1+2x) \sim 2x$,因此:
$$\lim _{x\rightarrow 0}\dfrac {\dfrac {1}{3}{x}^{3}}{{x}^{2}\ln (1+2x)}=\lim _{x\rightarrow 0}\dfrac {\dfrac {1}{3}{x}^{3}}{{x}^{2}2x}$$
$$=\lim _{x\rightarrow 0}\dfrac {\dfrac {1}{3}{x}^{3}}{2{x}^{3}}$$
$$=\dfrac {1}{6}$$