题目
10.(1995.Ⅲ)设 ((x)^2-1)=ln dfrac ({x)^2}({x)^2-2}, 且 [ varphi (x)] =ln x, 求 (int )_(varphi (x)dx)..

题目解答
答案
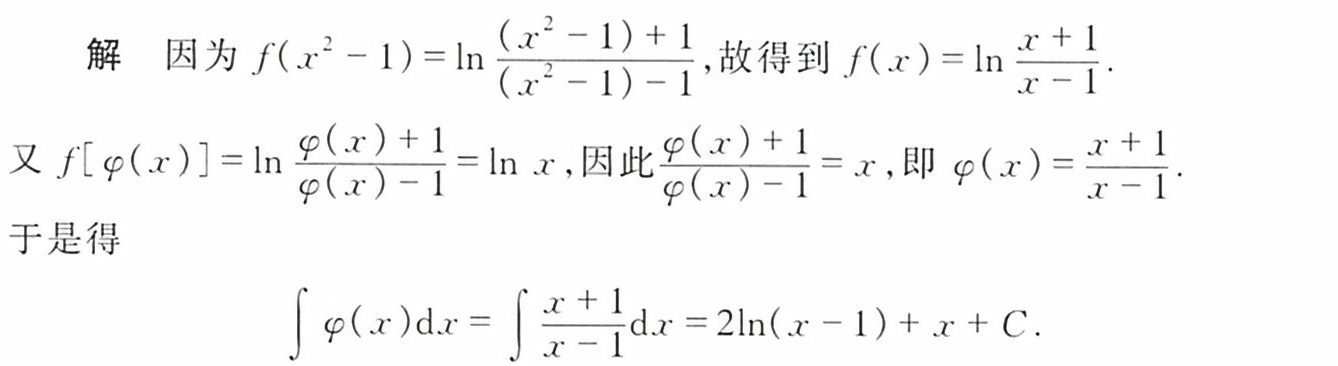
解析
考查要点:本题主要考查函数的复合与反解,以及分式函数的积分方法。
解题思路:
- 确定函数$f$的表达式:通过变量替换,将已知的$f(x^2 -1)$转化为关于$t = x^2 -1$的表达式,从而得到$f(t)$。
- 求解$\varphi(x)$:利用$f[\varphi(x)] = \ln x$,代入$f$的表达式,解分式方程得到$\varphi(x)$。
- 积分计算:将$\varphi(x)$分解为简单分式,利用积分公式求解。
破题关键:
- 变量替换是确定$f(x)$的核心步骤。
- 分式方程的解法需注意交叉相乘和代数变形。
- 分式分解简化积分过程,避免复杂计算。
步骤1:确定函数$f(x)$的表达式
设$t = x^2 - 1$,则$x^2 = t + 1$。代入原式:
$f(t) = \ln \frac{t + 1}{(t + 1) - 2} = \ln \frac{t + 1}{t - 1}$
因此,$f(x) = \ln \frac{x + 1}{x - 1}$。
步骤2:求解$\varphi(x)$
由$f[\varphi(x)] = \ln x$,代入$f$的表达式:
$\ln \frac{\varphi(x) + 1}{\varphi(x) - 1} = \ln x$
去掉对数得:
$\frac{\varphi(x) + 1}{\varphi(x) - 1} = x$
交叉相乘并整理:
$\varphi(x) + 1 = x(\varphi(x) - 1) \implies \varphi(x) = \frac{x + 1}{x - 1}$
步骤3:计算$\int \varphi(x) \, dx$
将$\varphi(x) = \frac{x + 1}{x - 1}$分解为:
$\frac{x + 1}{x - 1} = 1 + \frac{2}{x - 1}$
积分得:
$\int \varphi(x) \, dx = \int 1 \, dx + 2 \int \frac{1}{x - 1} \, dx = x + 2 \ln |x - 1| + C$